周波数カウンターとは
周波数カウンターは、入力信号の周波数を精確に測定するための電子計測器で、研究やエンジニアリングの分野で広く使用されています。このページでは、周波数カウンターの基本的な測定原理と、1970年代からの技術進化を解説します。特に、4世代にわたる周波数カウンターの特徴や、それぞれの測定方法の違いを詳述します。さらに、最新技術を搭載した周波数カウンターの選び方や測定上の注意点についても触れ、正確な周波数測定のための知識を提供します。
はじめに
周波数カウンターは、入力信号の周波数を測定する電子機器です。周波数は、周期信号の 1 秒あたりのサイクル数として定義され、ヘルツ (Hz) 単位で測定されます。
現在は多くの研究者やエンジニアにより使用される基本的な計測器となっております。
しかし、その設計は初めての製品が市場に投入されて以来、いくつかの進化を経ております。
1世代 1970年代 ダイレクトカウンター
2世代 1980年代 レシプロカルカウンター
3世代 1990年代 補間レシプロカルカウンター
4世代 2000年代 回帰分析付連続タイムスタンピングカウンター
本ページでは上記4世代の周波数カウンターの周波数測定原理、および測定上の注意点などについて解説させていただきます。
平均周波数
周波数カウンターで測定される周波数は規定時間（ゲート時間）内の平均周波数です。周波数カウンター原理を解説する前に、平均周波数の概念を整理させていただきます。
たとえ理想的とみなすことができる信号でも、現実の世界ではノイズの影響を受け、個々の周期が変化します。平均周波数の定義では信号サイクルを整数回（最低でも1 回）測定する必要がございますが、わずかなサイクル数の測定では信号の周波数を明らかにすることは困難です。また実在の多くの信号は定常的な周波数をもたない、変調された信号や周波数ホッピング信号、スイープ周波数信号、バースト信号周波数などがその例にあたります。
このため平均周波数の概念はこれらの信号に関しては有効ではないため、3項から6項では、周波数の安定した定常的な信号を測定することを前提として解説させていただきます。
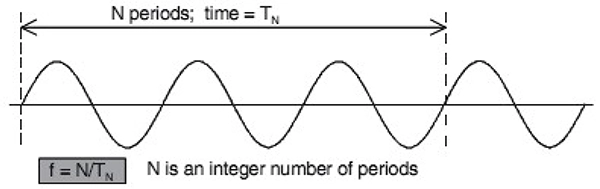図1. 平均周波数の定義
ダイレクトカウンター
ダイレクトカウンターは最も古い第1世代の周波数カウンターです。ダイレクトカウンターの原理として、規定時間ゲートを開き、その間入力サイクルのトリガーイベントを計測いたします。そのゲート時間が正確に1 sであれば、測定したサイクル数をほぼ周波数とみなすことができます（cycles/s）。ゲート時間の確度は外部、もしくは内部に搭載された水晶発振器（通常 10 MHz信号）に依存します。
しかし、ゲート時間は入力信号と非同期であるため、 測定結果は（2）式の平均周波数の定義を満たしておりません。そのため測定値には± 1サイクルの不確かさが含まれます。ゲート時間が1 sの場合、全ての入力信号周波数に対する分解能は1 Hzとなります。分解能を向上させるためにはゲート時間を増加させる必要がございます。例えばゲート時間を1 sから10 sにすることで、カウンターの分解能は0.1 Hzとなり、周波数カウンターの表示桁数が1桁向上致します。図2にダイレクトカウンターの分解能を記載します。上記の通り、分解能は入力信号周波数とゲート時間に依存いたします。
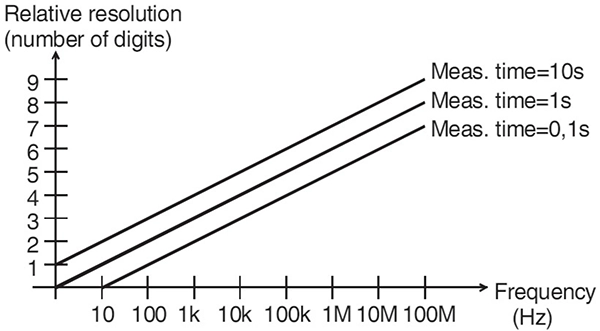図2. 周波数(Hz) vs分解能(桁数)vsゲートタイム(s)の関係
レシプロカルカウンター
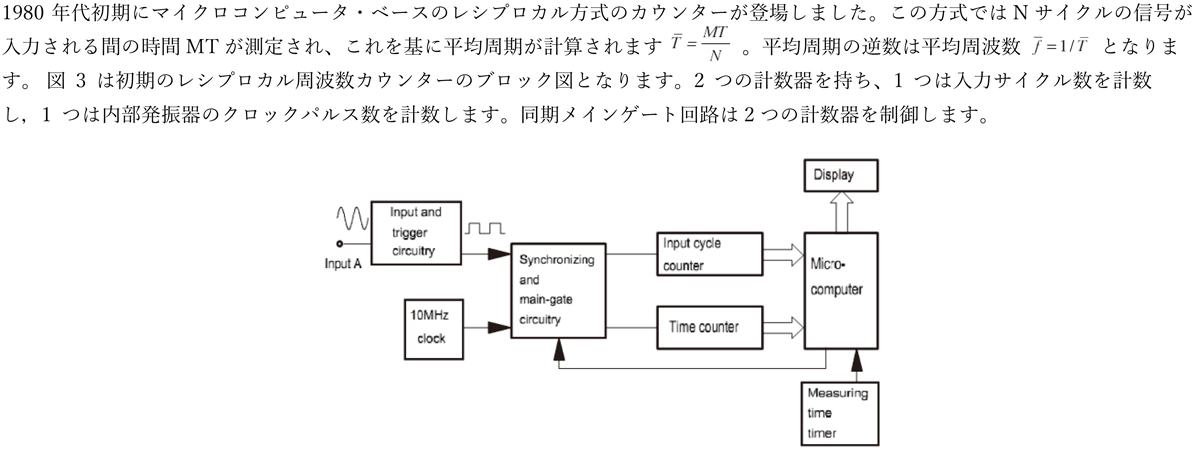図3. レシプロカルカウンターのブロックダイアグラム
ダイレクトカウンターと異なり、レシプロカルカウンターで設定された測定時間はゲート時間と一致しません。測定時間はマイクロコンピュータによって設定されますが、実際の測定時間MTは入力トリガーに同期いたします。入力サイクル数の測定値は正確であり、± 1サイクルエラーを回避可能です。切り捨てエラーはクロック計数において発生します（± 1クロックパルス）。平均周波数は式（4）で表され、tcは1クロック周期です。
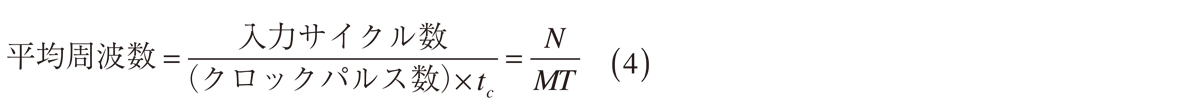
計算結果の分解能は± tc /MTで、10 MHzの内部発振器の場合± 100 ns/MTとなります。図4にレシプロカルカウンターの分解能を記載します。分解能は入力信号の周波数に依存はしなく、ゲート時間により変化いたします。
内部クロック周波数を高くすることで分解能を向上させることが可能です。例えば基準クロック周波数を100 MHzにすると分解能は± 10 ns/MTとなり、10 MHzクロック使用時と比べ周波数カウンターの分解能が1桁向上します。
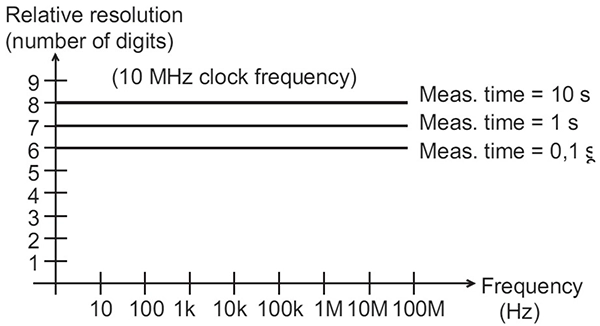図4. 周波数(Hz)とレシプロカルカウンターの分解能(桁数)の関係
補間レシプロカルカウンター
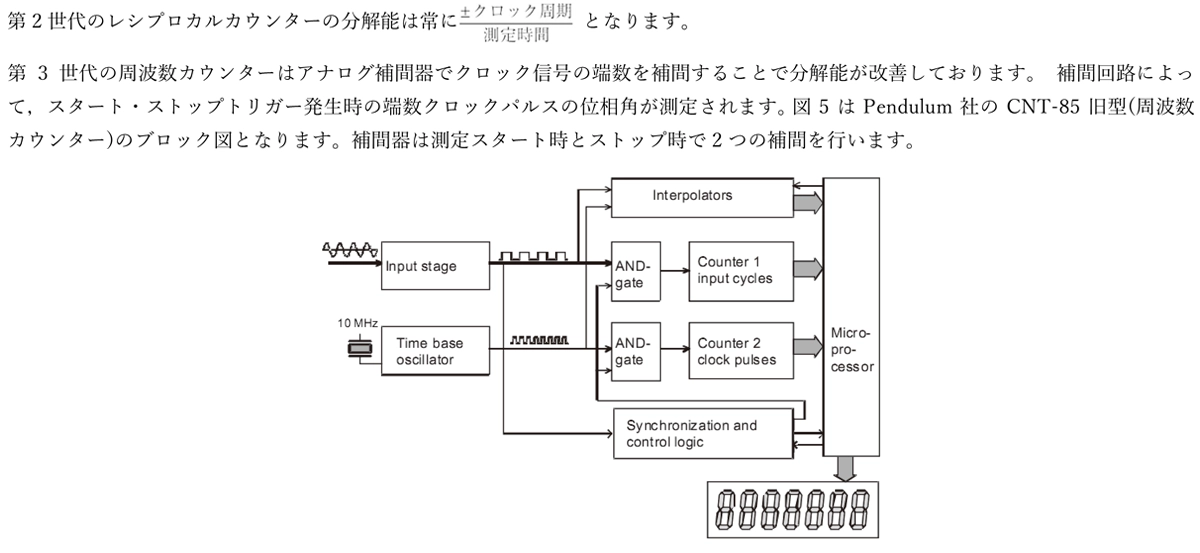図5. 補間レシプロカルカウンターのブロックダイアグラム
図6は補間器の原理でスタートトリガーと次のクロックパルス間、およびストップトリガーと次のクロックパルス間の短い端数時間を測定しております。図6のアナログ補間器はトリガーイベント発生後、クロックパルスが2回発生するまで一定の電流Iでコンデンサーを充電します。
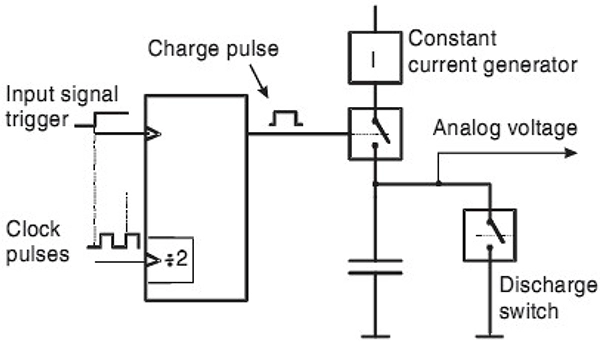図6. アナログ補間器の基本原理(時間から電圧への変換)
この間コンデンサーはQ（t）= I · tで充電されます。容量Cのコンデンサーに生じる電圧U（t）は式（5）で表されます。
チャージ時間（t）の値は1から2クロック周期に相当する値で通常100～200 nsの間で変化いたします。U（t）もU0（ 1クロック周期での値）と2U0（2クロックサイクル）の間で変化します。U（t）の電圧値を測定することで端数時間を測定いたします。
計数されたサイクル数Nは正確な整数であり、第2世代のレシプロカルカウンターと同等ですが、時間MTの確度が大幅に改善されております。また、± 1クロック周期であった分解能が、補間器の導入によってクロック周期の1%未満まで改善されてます。MTはTN + T1－T2で計算可能です。TNはクロックがサイクル数をN回刻むのに要する時間、T1は補間器で得られたスタートトリガーと次のクロックパルス間の端数時間、T2はストップトリガーと次のクロックパルス間の端数時間となります。
補間レシプロカルカウンターの出現により、測定分解能は第2世代の周波数カウンターと比較して約100～400倍改善しました。一般的な10 MHz発振器ベースの補間レシプロカルカウンターで、分解能は100 nsから1 nsに改善しております。
回帰分析付連続タイムスタンピングカウンター
補間の有無に関わらず、レシプロカルカウンターの周波数測定は、あらかじめ設定されたスタート（スタートトリガーイベント）とストップ（ストップトリガーイベント）間で行われます。測定ストップから次の測定スタートの間には、測定結果の出力、レジスタのリセット、次の測定準備のための避けられないデッドタイムが存在します。連続タイムスタンピングカウンターはこの点を改善することは可能です。
タイムスタンピングカウンターは、入力信号トリガーイベントとクロック周期を連続的にリセットすることなくカウントします。一定の間隔（ペーシング間隔）で、イベントカウントレジスタと時間カウントレジスタの瞬時値がメモリに転送されます。各レジスタの読み取りは常に入力トリガーに同期し、これがタイムスタンプのトリガーイベントとなります。各タイムスタンプの値は分解能向上のため補間されております。メモリに保存された値は後処理されます。1秒間の周波数測定においてレシプロカルカウンターの様にスタートイベントパルス、ストップイベントパルスのみを測定するのではなく、数百～数千のタイムスタンプイベントが測定されます。
測定時間MTにおいて最も理想的な平均周波数を得るための直線y = a + b · (x－x0）は図7で示している最小2乗法を使用した線形回帰で算出されます。ここでは、
x = イベントカウントの累計（独立変数）
y = サンプルポイントでの時間（従属変数） a = x = x0での初期値
b = f *－1 = T *となります。
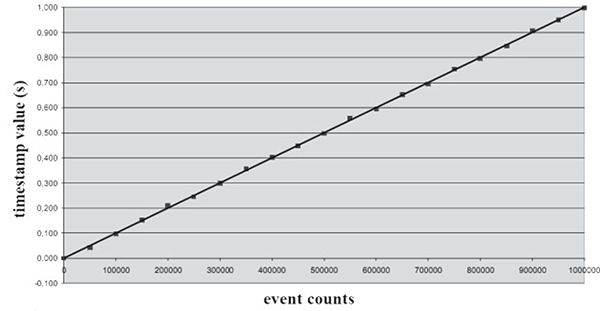図7. 測定開始/停止間のトリガーイベントのタイムスタンプ
回帰線の傾きbは、入力信号の推定平均周期（T *）と一致しT *は式（6）で表されます。
そして傾き（b またはT *）の分散は式（7）で表されます。
（s y）はykの不確かさtRESである．（s x）は独立な確立変数Xの標準偏差であり、確立変数Xはx0からx0 + Nのレンジで全区間内に一様に分布するサンプルが線形に増加すると見なすことができ、式（8）で表されます。
ここでNは計数されたサイクル数でnはサンプル数となります。nが十分大きければ確立密度関数は式（9）で表されます。
平均µ と分散σ 2は式（10）、（11）で表されます。
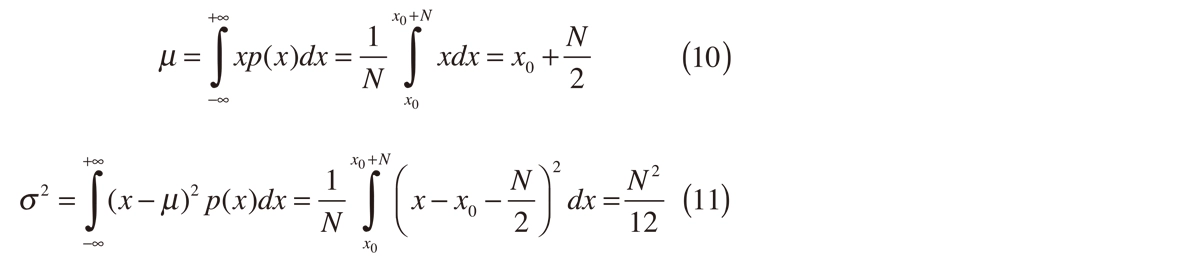
またT * = MT/N、（s y）= tRESであることから式（7）は式（13）となります。
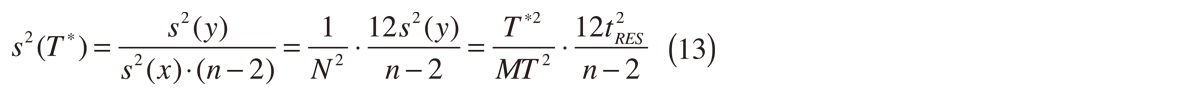
式（13）によりクロック周期および周波数の不確かさは式（14）で与えられます。
図8は第4世代の周波数カウンターとして、世界で最初にリリースされたPendulum社のCNT-90 型周波数カウンターです。
図8. Pendulum Instruments社 周波数カウンター/アナライザ CNT-90
この製品の仕様ではtRES = 70 psでnは最大1000です。
nの値は測定時間MTに依存し、800/MTとなります。理想的な矩形波を測定した場合、MT = 1 sでの周波数分解能は（16）式となります。
スタート・ストップ法での分解能と比較して分解能が向上しております。
CNT-90は自動測定モードを持っており、回帰法は測定時間が200 ms以上の場合、それが選択される一方、それより測定時間が短い場合は、スタート・ストップ法が選択されます。図9にスタート・ストップ法と自動測定モードでの分解能を記載します。分解能は、測定時間が0.2から100 sの間で改善します。MTが増加してもハードウェア上の制約でnが最大1000に制限されるため100 s以上では回帰法とスタート・ストップ法の分解能は同等となります。
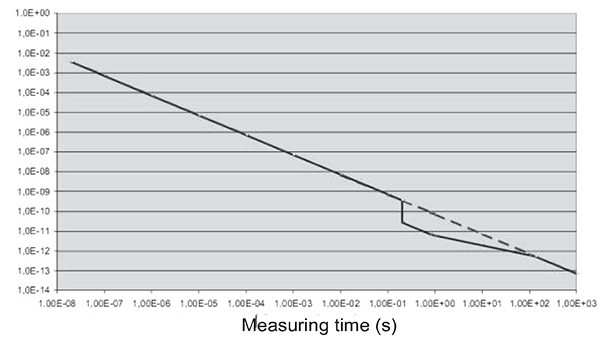図9. 連続タイムスタンピングカウンターCNT-90の分解能
※線形回帰による分解能の向上は、200msから最大 100sまでの測定時間 (自動モード) で発生します。
測定上の注意
線形回帰は測定時間の間、周波数が名目上一定と仮定します。この方法は、測定する過程でのランダムな変化やノイズを減らすのに良いですが、入力信号が強く変調されているか、かなりのドリフトがある場合（例えば周波数スイープ）、スタート・ストップ手法の方が信号の平均周波数をより正確に得られます。図10は過度の周波数ドリフトがある場合の回帰直線です。回帰直線の傾きがスタート・ストップ間の直線（= 平均周波数）から外れております。
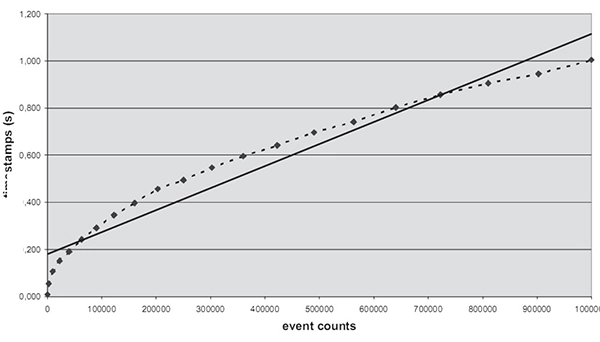図10. 周波数ドリフトがある場合の回帰直線
※分解能は向上しません。
