時間間隔測定の決定版~不確かさ排除の完全ガイド: CNT-104S

CNT-104Sは、4つの並列入力信号を同時に測定できるマルチチャンネル周波数/時間間隔アナライザです。 測定機能の1つに、タイムスタンプ解像度が7ps未満の従来のタイムインターバル測定があります。この技術仕様書では、時間間隔測定における不確かさの要素と、チャンネル間で生じるスキュー(時間的なずれ)を排除するための校正方法について説明します。
1.時間間隔測定における不確かさの要因
タイマー/カウンターによる時間間隔測定には、モデルによって異なる不確かさが伴います。従来これらの不確かさの要因は、以下の2に分けられます。
- 平均によって低減できる「偶発的」不確かさ
- 平均によっては低減できない「系統的」不確かさ
「偶発的」不確かさ
「偶発的」不確かさには、量子化誤差(分解能)とノイズトリガー誤差の2つがあります。
分解能とは、2つの値がいかに接近していても、それぞれを区別して認識できる能力のことです。これは通常、固定された非常に安定した時間間隔を多数のサンプルで測定した際に現れる、機器自身の測定値のばらつき(標準偏差)として定義されます 。
時間間隔は『開始トリガー』と『停止トリガー』で構成されるため、機器の分解能の概念は、それぞれのトリガー点におけるばらつき、つまり『タイムスタンプあたりの分解能』と言及されるのが一般的です。開始トリガーと停止トリガーの両方のばらつきを含む全体の時間間隔測定の分解能は、タイムスタンプあたりの分解能に、√2 (=1.4)を掛けることで求められます。
Pendulum CNT-104Sの場合、タイムスタンプあたりの分解能は7ps rms未満であり 、完全な時間間隔測定の分解能は10ps rms未満です。
同じ時間間隔を繰り返し測定する場合、内蔵の統計機能を利用することで、サンプル数の平方根に比例して「偶発的」不確かさを低減することができます。
例えば、100サンプルを使用すると分解能の不確かさは10分の1に、100万サンプルを使用すると1000分の1にまで低減可能です。
繰り返し行われる時間間隔測定の分解能は、十分に多くのサンプル数を用いることで、事実上ゼロにまで常に低減できます。
外部または内部ノイズによって引き起こされるノイズトリガーエラーは、もう一つの「偶発的」不確かさの要因です。これは、トリガーポイントのスルーレートが低い信号、例えば低周波の正弦波において顕著になります。
ノイズの不確かさ
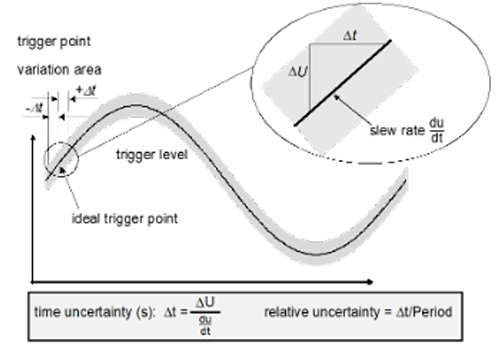
例1: 100Hz, 1Vrmsの正弦波に、外部および内部ノイズ源からの0.5mVrmsのホワイトノイズが加わると、時間的不確かさは約1µsのオーダーになります。これは、分解能の不確かさである7psと比較して非常に大きい値です。
例2: 同じく上記の0.5mVrmsの増幅器ノイズを持つ、立ち上がり時間4nsの0Vから5Vのパルスでは、時間的不確かさはおよそ0.5ps rmsになります。これは、分解能の不確かさである7psと比較して小さい値です。
このランダムなトリガーノイズ誤差も、分解能の不確かさと同様に、平均化によって低減できます。
立ち上がりの速いパルス(立ち上がり時間5ns未満)でスルーレートが高い場合(1V/ns超)、ノイズトリガー誤差は分解能の不確かさよりも一桁小さくなるため、無視できるでしょう。
「系統的」不確かさ
時間間隔測定には、3種類の「系統的」不確かさの要因あります。それは、タイムベース誤差、トリガーレベル設定誤差、そしてチャネル間オフセット誤差です。
タイムベース誤差は、主に経年変化や温度の影響によって生じ、時間間隔測定に系統的な誤差をもたらします。この誤差は、非常に長い時間間隔では顕著になりますが、短い時間間隔では完全に無視できます。
例1: TCXO(温度補正型水晶発振器)のリファレンス発振器は、1ppm(10−6)未満の誤差を持つ場合があります。これは1秒の時間間隔では1µsの系統誤差に相当しますが、1μsの間隔ではわずか1psにしかなりません。
例2: 超安定OCXO(恒温槽付水晶発振器)のリファレンス発振器は、10ppb(10−8)未満の誤差を持つ場合があります。これは1秒の時間間隔では10nsの系統誤差に相当しますが、1μsの間隔ではわずか10fsにしかなりません。
1 μs未満の短い時間間隔では、あらゆるリファレンス発振器においてタイムベース誤差は無視できます。また、超安定OCXOの場合、100 μs未満の時間間隔ではタイムベース誤差は無視できます。
トリガーレベルの設定誤差は、実際のトリガーレベルが意図したレベルと異なる場合に発生します。例えば、パルス幅を測定する際は、立ち上がりエッジと立ち下がりエッジにおける振幅の50%点を用いるのが一般的です。従来のカウンターでは、CNT-104Sの入力が持つ約20mVのヒステリシス帯域により、10mVものトリガーレベルオフセットが生じる可能性がありました。しかし、CNT-104Sは自動ヒステリシス補正機能を搭載しているため、実際のトリガー点は設定レベルから通常わずか2mVしかずれません。この不確かさは、スタートとストップの両トリガーポイントで確認されます。なお、立ち上がりの速いパルスであれば、この誤差成分は無視できるでしょう。
例: 立ち上がり時間4nsの0Vから5Vのパルスでは、約2psの時間的不確かさをもたらします。
立ち上がりの速いパルス(立ち上がり時間5ns未満)でスルーレートが高い場合(1V/ns超)は、トリガーレベル設定誤差は無視できます。
チャネル間オフセット誤差は、通常100ps rmsです。この測定不確かさは、入力コネクタから、スタートチャネルとストップチャネルそれぞれのトリガーイベントが実際に内部タイムスタンプ処理に至るまでの伝播時間の差に起因します。この信号経路には、入力増幅器の伝播時間、各チャネル内のコンパレータでの遅延、そしてタイムスタンプ回路に至るまでのFPGA内部の遅延が含まれます。
チャネル間オフセットは、特定の測定においては固定値ですが、入力増幅器の設定、時間間隔の値、入力信号の周波数、および入力信号の振幅によって測定ごとに変動します。CNT-104Sでは、一部の標準信号を用いて内部的に校正されており、その残差の不確かさは100ps rmsです。
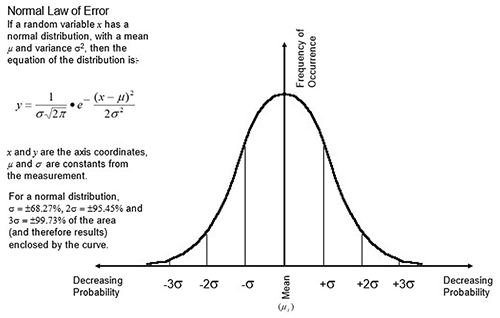
100ps rmsとは、全てのオフセットのうち68%が±100ps(1シグマ)の範囲内に収まり、95.5%が±200ps(2シグマ)の範囲内に収まることを意味します。
チャネル間オフセット誤差は、パルス間の短い時間間隔(1ms未満)では主要な系統誤差要因となりますが、長い時間間隔(10ms超)では無視できます。
結論: 時間間隔の不確かさについては5つの異なる誤差源を特定しましたが、一般的な使用ケースにおいては、そのほとんどを排除することが可能です。
概略: 「偶発的」不確かさは、平均化によって非常に小さな値まで低減できるため、「系統的」不確かさに比べて無視できるレベルとなります。
「偶発的」不確かさについて:
立ち上がりの速いパルス: ノイズトリガー誤差を考慮する必要がありません。
低周波正弦波: ノイズトリガー誤差が大半を占めます。分解能は無視できます。
繰り返しパルス: 分解能は常に平均化によって低減できるため、常に無視して構いません。
「系統的」不確かさ
- 非常に長い時間間隔: チャネル間オフセットは考慮不要です。タイムベース誤差が大半を占めます。
- 非常に短い時間間隔: タイムベース誤差は考慮不要です。チャネル間オフセットが大半を占めます。
- 立ち上がりの速いパルス: トリガーレベル設定誤差は考慮不要です。
- 立ち上がりの遅いパルス、または低周波の正弦波/三角波: トリガーレベル設定誤差が大半を占めます。
2.「系統的」チャネル間オフセットの校正方法
通常100 ps rms程度のチャネル間オフセット誤差は、平均化では低減できません。しかし、正確に校正して補正することは可能です。
方法1:カウンターの入力に既知の0 nsの時間間隔信号を送り、その測定結果を読み取ります。その後、MATH機能を使って測定された時間間隔を補正します。
注意点: 校正信号の振幅と繰り返し周波数は、最終測定で使う実際の信号にできる限り近いものにしてください。入力増幅器のパラメーターは変更してはいけません。
時間間隔が0(ゼロデッドタイム)の信号を生成する最も簡単な方法は、最終テスト周波数と同じ周波数の高速立ち上がりパルス列をパワースプリッターに接続し、その後、同じ長さのケーブルで入力Aと入力Bに供給することです。なお、CNT-104Sのパルス出力を使えばより簡単に行えます。
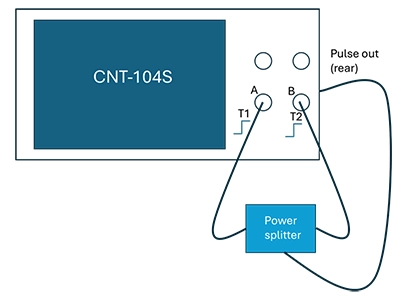
この方法はシンプルですが、パワースプリッターとケーブルの伝播時間には避けられない不確かさが伴います。例えば、例えば、ケーブルの長さがわずか2 mm異なるだけで伝播時間に10 psの差が生じることを考えると、その不確かさは10〜20 ps程度になります。さらに、CNT-104Sの振幅が実際にテストで使用するパルス源と異なる場合があり、ゼロインターバル校正は短い時間間隔では非常に正確でも、長い時間間隔では精度が低下する可能性があります。
方法2:カウンターの入力で未知の時間間隔(T2-T1)を測定し、その結果を読み取ります。これは、ディスプレイに表示される値が、未知の時間間隔(T2-T1)と内部信号経路の差(DELAY(B) – DELAY(A))を合わせた結果(TB – TA) であることを意味します。
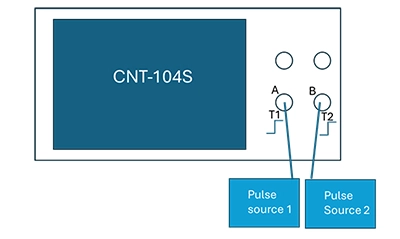
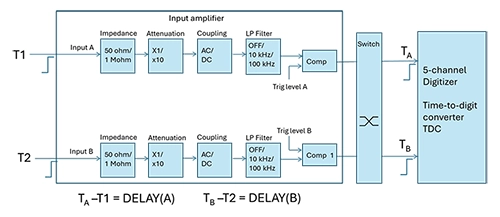
ご存じのとおり、測定の不確かさは通常100 psとされています。次のステップとして、外部のケーブルを入れ替えます。もし内部的なチャネル間オフセットがなければ、この操作で理論上は同じ値で符号が逆になるはずです。例えば、タイムインターバルが1.5 nsだった場合、理想的なカウンターであれば、ケーブルを入れ替えた後には-1.5 nsと表示されるでしょう。 しかし、内部のチャネル間オフセットがあるため、ケーブルを入れ替えた後の測定値は異なります。測定値1から測定値2を引いて2で割ることで、補正されたタイムインターバル値が得られます。
Reading 1:
TB–TA=(T2+DELAY(B))–(T1+DELAY(A))
Reading 2:
TB–TA=(T1+DELAY(B))–(T2+DELAY(A))
Reading 1 – Reading 2 =
=(T2+DELAY(B))–(T1+DELAY(A))–[(T1+DELAY(B))–(T2+DELAY(A))]
=T2–T1–T1+T2=2×(T2–T1)
したがって、正しい時間間隔のCalculatedは以下の通りです。
[(Reading 1–Calculated2)]/2
この後、系統誤差である DELAY(B)–DELAY(A) は、以下のように求められます。
Reading 1 – Calculated (T2–T1) =
=(T2+DELAY(B))–(T1+DELAY(A))–(T2–T1)=DELAY(B)–DELAY(A)
あるいは、系統誤差はReading 1とReading 2の平均として求めることもできます。
系統的オフセット誤差は [(Reading 1+ Reading 2)]/2 となります。
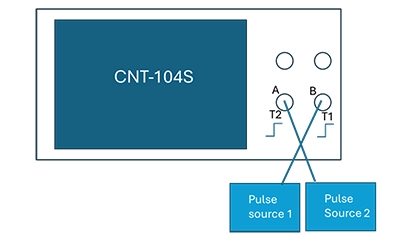
例1: 約10nsの差がある場合
最初のReadingが10.250 ns、ケーブルを交換した後の2番目のReadingが-9.950 ns だったとします。
Caluculated時間間隔は次のとおりです。 [10.250−(−9.950)]/2=10.100 ns
この場合の系統誤差は、次のように算出されます。
[(Reading 1)−(Calculated時間間隔)]=10.250−10.100=150 ps
この系統誤差は、測定した時間間隔をMATH機能で補正することで取り除けます。
- MATH機能で K*X を選択します。
- K = 1 に設定します。
- L = -150 ps に設定します。
例2: 約0nsの差がある場合
最初のReadingが -248 ps、ケーブルを交換した後の2番目のReadingが -68 ps だったとします。
正しい時間間隔のCalculatedは次のとおりです。
[−248−(−68)]/2=−180/2=-90 ps
この場合の系統誤差は、次のように算出されます。
[(Reading 1)−(Calculated時間間隔)]=−248+90=-158 ps
この系統誤差は、測定した時間間隔をMATH機能で補正することで取り除けます。
- MATH機能で K*X を選択
- K = 1に設定
- L = +90 ps に設定
注記: タイムベース誤差以外の系統誤差には、トリガーレベルのタイミング誤差や、入力からFPGA内のデジタイザまでの伝播時間差が含まれます。この校正方法は、これらの両方の誤差源を補正します。
ごくわずかな残差誤差が残りますが、これは10 ps未満となるはずです。
CNT-104Sを用いた不確かさの例 1:
この例では、約1nsの時間間隔を測定します。パルス出力の繰り返し周波数は1MHz、振幅は2.5V、立ち上がり時間は2.5nsです。CNT-104Sは標準のTCXO(不確かさ1ppm)を搭載し、校正のために10,000サンプルを平均します。外部および内部入力のホワイトノイズは0.5mV rmsと仮定します。
「偶発的」不確かさ:
- 分解能:シングルショット時10 ps rms, 10,000サンプル平均時100 fs rms
- ノイズトリガー誤差:シングルショット時0.9 ps rms, 10,000サンプル平均時:9 fs rms
「系統的」不確かさ:
- タイムベース誤差: < 1 fs(1ns * 1ppm)
- トリガーレベルタイミング誤差:校正なし< 18 ps, 校正あり< 10 ps
- チャネル間オフセット:校正なし100 ps rms, 校正あり< 10 ps
校正後、全体の不確かさは約10 psのオーダーになります。
CNT-104Sを用いた不確かさの例 2:
この例では、約100µsの時間間隔を測定します。パルス繰り返し周波数は1kHz、振幅は2.5V、立ち上がり時間は2.5nsです。CNT-104Sには標準のTCXO(不確かさ1ppm)が搭載されています。校正のために100サンプルを平均します。外部および内部入力のホワイトノイズは0.5mV rmsと仮定します。
「偶発的」不確かさ:
- 分解能:シングルショット時10 ps rms, 100サンプル平均時1 ps rms
- ノイズトリガー誤差:シングルショット時0.9 ps rms, 100サンプル平均時90 fs rms
「系統的」不確かさ:
- タイムベース誤差:< 100 ps(100µs * 1ppm)
- トリガーレベルタイミング誤差:校正なし< 18 ps, 校正あり< 10 ps
- チャネル間オフセット:校正なし100 ps rms, 校正あり< 10 ps
校正後、全体の不確かさは約100 psのオーダーになります。
3.理論的背景
不確かさの種類と用語
すべての測定値には、その値に不確かさが伴います。測定結果は、測定対象物自体のばらつき、温度などの環境要因、ノイズやケーブルの反射といったシステム要因、そして測定器自身の不確かさによって変動する可能性があります。
国際的な慣例に従い、この不確かさの要因は以下の2つのグループに分類されます。
- タイプAもしくは「偶発的」:
- 統計的手法で評価され、偶発的な影響を受けるもの
- タイプBもしくは「系統的」:
- その他の手法で評価され、系統的な影響を受ける可能性のあるもの。
「偶発的」不確かさ(タイプA)
- 量子化誤差(分解能)
- 機器ノイズ
- 測定「システム」ノイズ
- 再現性
これらの不確かさは、二乗平均平方根(RMS)アプローチを使って結合されます。複数の偶発的な要素を組み合わせると、結合された結果は正規分布(ガウス分布)に近づきます。
「偶発的」不確かさの結合
(s = 標準偏差)
uR=(s12+s22+s32+…)
正規分布では、曲線で囲まれた面積(および結果)のσ=±68.27%, 2σ=±95.45%, 3σ=±99.73%がそれぞれ該当します。
「RMS」と指定されたランダムパラメータは、「1シグマ信頼度」を持つと見なされ、これは全結果の68%がRMS仕様の範囲内にあることを意味します。
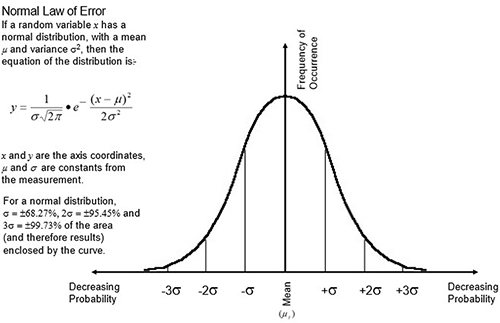
「系統的」不確かさ(タイプB)
- 補正されていない誤差
- 誤差補正後の残留誤差
- 時間や温度に対する安定性
- 直線性および電力に関連する誤差
- 機器設定誤差
- オペレーターのバイアス
データシートに記載されているタイプBの誤差は、通常、製造業者が規定された範囲内に値が収まることを保証する「限界値」として提示されます。不確かさを正しく扱うためには、これらの限界値を標準偏差に変換する必要があります。
ほとんどの「系統的」不確かさでは、±αの範囲内で「矩形分布」を仮定できます。矩形分布では、その範囲内のすべての値が等しい確率を持つと仮定され、関連する標準偏差は α/√3 となります。
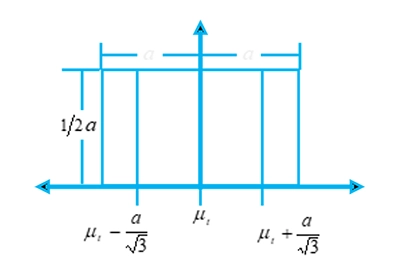
矩形分布では、矩形確率限界内であれば、どの位置でもサンプルが発生する確率は等しいと考えられます。
「系統的」不確かさの結合
(α = 限界値)
uS=((a12+a22+a32+…)/3)
「偶発的」不確かさと「系統的」不確かさの結合 - まとめ
- 既知のすべての誤差源を特定する
- タイプA(ランダム)とタイプB(系統的)に分離する
- 実行可能であれば補正を適用する(タイプB)
- タイプA標準不確かさ (uR) を計算する uR=(s12+s22+s32+…)
- タイプB標準不確かさ (uS) を計算する uS=((a12+a22+a32+…)/3)
- ランダム不確かさと「系統的」不確かさを結合する U=(uR2+uS2)
- k=2 に対する拡張不確かさを計算する、または標準的な計量学の実践に従い 2×U を算出する
