ミリ波レーダーの基礎2 [スペックについて]



ミリ波レーダーのスペック
ミリ波レーダーを使いこなすには主に3つの性能を理解する必要があります。
- 距離分解能・最大検知距離
- 速度分解能・最大検知速度
- 角度分解能・最大検知角度
以降、順を追って説明します。
距離分解能・最大検知距離
距離分解能
距離分解能は2つ物標を分離して検知できる距離を表します(距離精度とは異なりますのでご注意ください)。
距離分解能は、

と定義されます。つまり、ミリ波の利用帯域幅に反比例することになります。
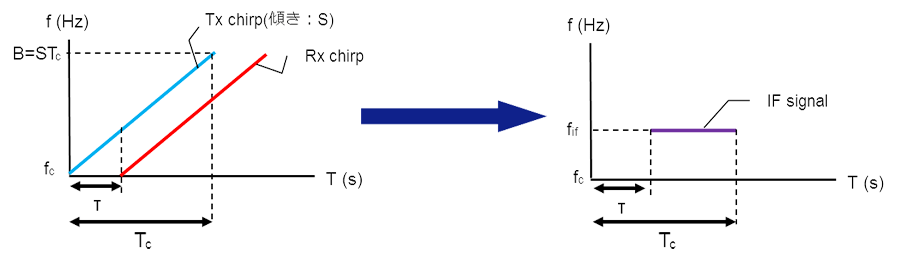 図1
図1
従来の24GHz帯(帯域幅250MHz)の場合、距離分解能は60cmとなり、例えば屋内向けの近距離レーダー用途には不向きです。しかし、79GHz帯(帯域幅が4GHz)の場合、距離分解能は3.75cmと非常に高い距離分解能を実現でき、様々なアプリケーションへの応用が可能となります。
最大検知距離
検知可能な最大距離についてはミリ波レーダー単体で決定されるものでなく、アンテナ部の設計や物標の素材や大きさ、形状など様々な要因から決定されます。主に以下の3つの要因で最大検知距離が決定されます。
- チャープ設計
- 物標のレーダー断面積(RCS)
- アンテナ設計
チャープ設計
ミリ波レーダーで測距を行う場合、チャープスロープ(傾き)によって距離が計算されます。IF信号の最大周波数fif_maxはチャープスロープSと最大検知距離Rmaxによって決定されます。
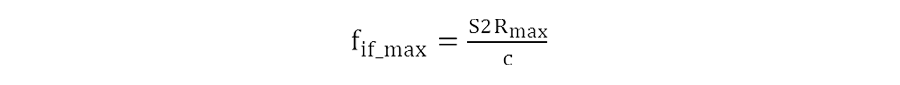
ミリ波レーダーでデータ処理を行う場合、IF信号をAD変換した後、後段の信号処理部へ出力します。そのため、ADCサンプリングレートFsは上記の最大周波数より大きい必要があります。
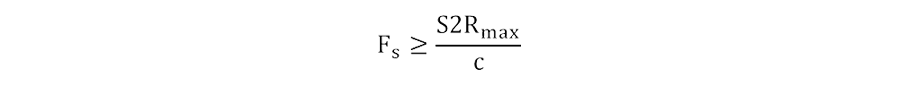
よって最大検知距離は、
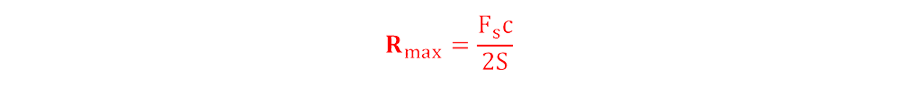
と定義されます。
つまり、サンプリングレートFsを高く、あるいはチャープスロープの傾きSを小さく設計することで最大検知距離を大きくすることが可能です。しかし、チャープスロープSに関しては、距離分解能Rresとトレードオフの関係になることに注意する必要があります。
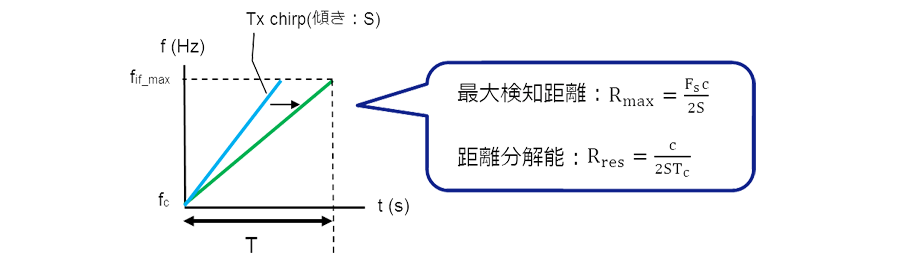 図2
図2
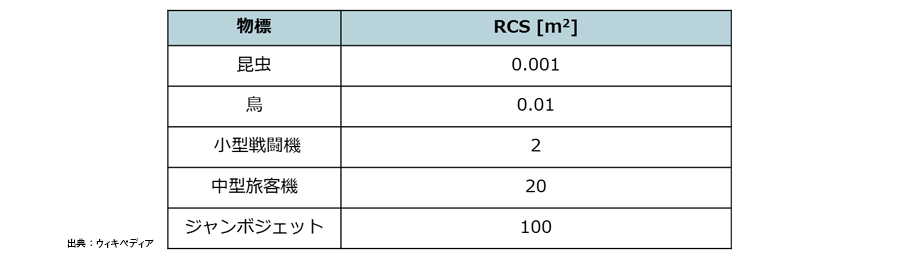
物標のレーダー断面積(RCS)
レーダー断面積(RCS)とは、照射された電波を受信アンテナ方向へ再放射する能力を表す指標です。RCSが高いほど、レーダーで検知しやすいということになります。
RCSは面積の単位で表せますが、物標の表面積だけではなく、形状や大きさ、電気的特性、電波の波長等によって決定される値となります。[1]
また、物標の表面の粗さによる散乱特性や透過特性もRCSに影響を与えます。[1]
RCSは一義的に決まらない変動量であるため、平均的な値で検討されることが多く、具体的な目安としては表1のようになります。
RCSを厳密に評価するには専門的な知識や設備が必要になりますので、レーダーモジュール評価キットを使用して実際に対象物を検知することができるかどうかを実験しながら仕様検討することをおすすめします。
アンテナ設計
アンテナ設計によっても最大検知距離は変わります。ここではTITAN T16のアンテナ設計の例(図3)をご紹介します。このように、アンテナ設計が異なることで検知距離が変わってきます。
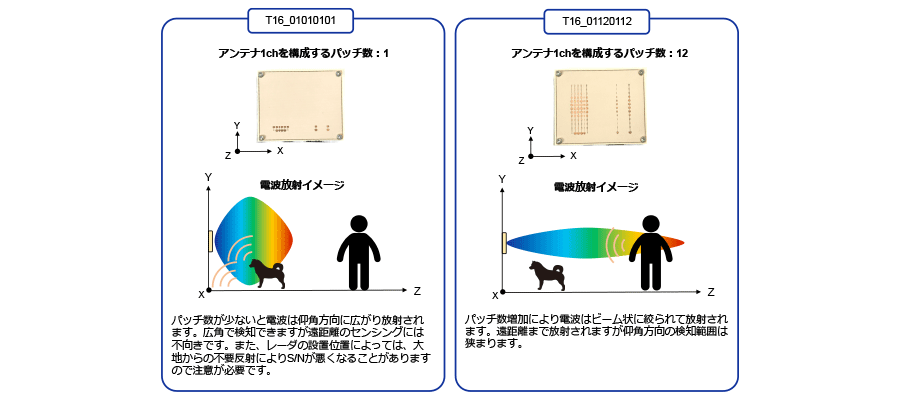 図3
図3
速度分解能・最大検知速度
速度分解能
速度分解能は、2つ物標を分離して検知できる速度差を表します。速度分解能は図4のようにドップラーFFT処理後のピーク間の位相差Δωから求められます。
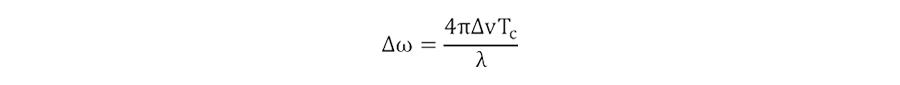
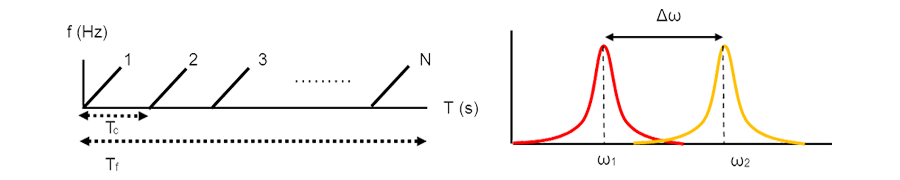 図4
図4
ここで、離散フーリエ変換の特性より、
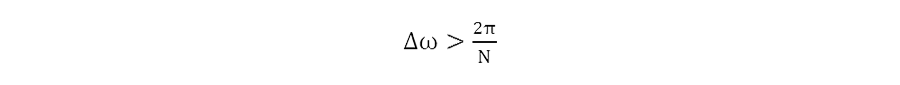
の条件が必要になります。よって速度分解能は、
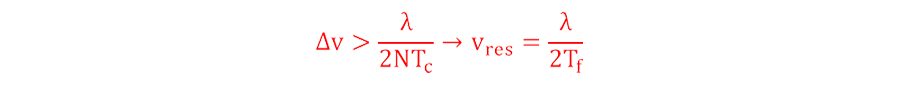
と定義されます。つまり、速度分解能は設定したフレーム時間Tfに反比例することになります。
最大検知速度
ここでは1つの物標に対し、2つのチャープを用いて速度検出を行う例を見ていきましょう。
ミリ波レーダーの基礎1 (詳しくはこちらから)で説明したように、速度はIF信号の位相差を検出し測定しています。このとき、測定時の曖昧さをなくすため、図5のように検出できる位相差は±π以下という条件が必要になります。
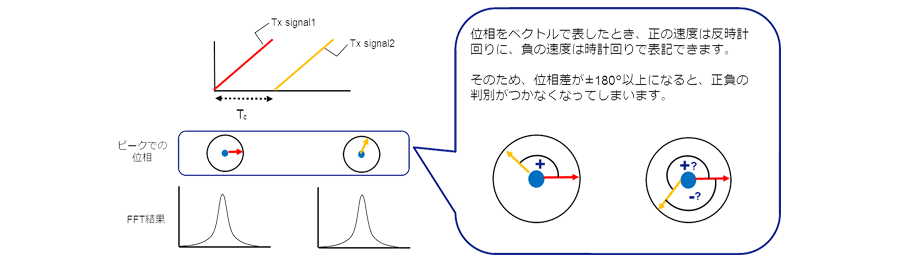 図5
図5
この条件を式で表すと以下のようになります。
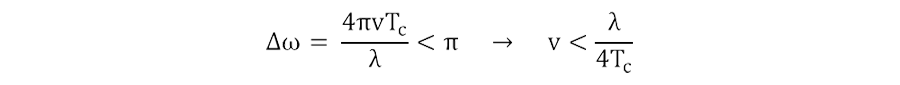
よって、最大検知速度vmaxは
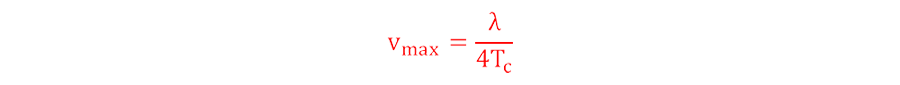
と定義されます。つまり、最大検知速度vmaxはチャープ持続時間Tcに反比例することになります。最大検知速度vmaxを大きくしたい場合、チャープ持続時間Tcを小さくする必要がありますが、図6のように距離・速度分解能とトレードオフになることに注意する必要があります。
 図6
図6
角度分解能・最大検知角度
角度分解能
角度分解能は、2つ物標を分離して検知できる角度を表しており、主にアンテナ部の設計が大きく関連します。角度を検知するには複数の受信アンテナが必要となるとミリ波レーダーの基礎1 (詳しくはこちらから)で説明しましたが、この受信アンテナ数を増やすことにより角度分解能を向上することができます。

例として、受信アンテナが8本の場合、角度分解能は14.3°となります。
しかし、受信アンテナを増やすことで角度分解能を向上できますが、システムやアプリケーションの肥大化を招くこととなり設計上あまり効率的ではありません。
そこで、省スペース化を実現しながら擬似的に受信アンテナ数を増やす技術として、MIMO(Multiple-input-multiple-output)を利用することができます。
MIMOとは?
MIMOは複数アンテナから信号を送信することで、実装されている受信アンテナ数以上の仮想受信アンテナを生み出すことができる技術です。図7のように、送信アンテナを2本、受信アンテナを4本用意したケースでMIMOの動きを見ていきましょう。
- Tx1から信号を送信、Rx1を基準に各受信アンテナではそれぞれ0、ω、2ω、3ωの位相差が発生。
- Tx2から同様に信号を送信すると、受信まで4dsinθ分の追加距離が生じ、Tx1と比較して4ω追加の位相差が発生。
よって、受信アンテナにおける位相差は4ω、5ω、6ω、7ωとなる。 - 2本の送信アンテナで位相差を8つ生成でき、これは送信アンテナ1本に対して受信アンテナ8本を用意することと同等の効果を得ることができる。
仮想アンテナの生成により、総アンテナ数を減らしつつ高角度分解能を実現できます。
MIMOを用いることで、送信アンテナ数 x 受信アンテナ数の仮想受信アンテナを得ることが可能です。
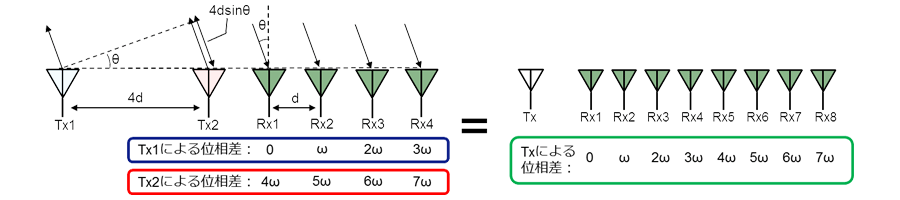 図7
図7
最大検知角度
検知できる最大角度についても分解能と同様に、アンテナ設計によりそのスペックが左右されます。
角度検知は、アンテナ間の位相差より、

と表すことができます。ここで、検知可能な最大位相差は±πとなるため、最大検知角度θmaxは
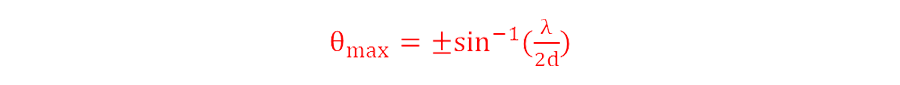
と定義されます。つまり、アンテナ間距離dをλ/2にすることでθmax=90°と最大化することができます。
まとめ
以上、レーダーのスペックに関する基礎知識をご紹介しました。
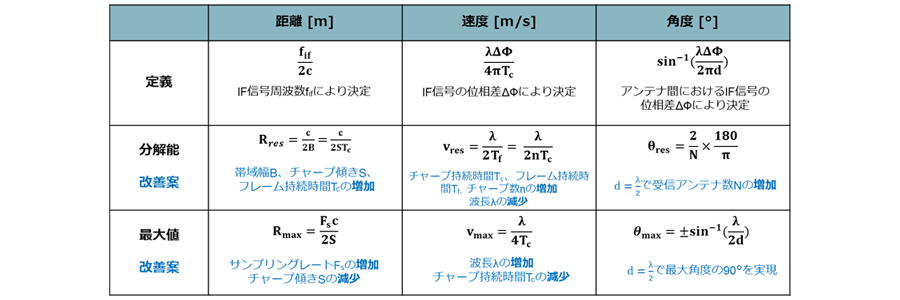
今回の内容を表3にまとめます。レーダーの性能を理解する上で重要なポイントになりますので、ぜひ覚えてください。
なお、いずれも理論値となり、実際は電波の減衰やノイズ等の影響を受けますので、レーダーモジュール評価キットを使用して実験しながら性能を確認していくと良いでしょう。
表3
参考文献
[1]梶原昭博, “ミリ波レーダ技術と設計 -車載用レーダやレーダ技術への応用-”, 科学情報出版(2019)