WPTと周波数 (3)

今回は前回に続き WPT とその周波数の特徴についてもう少し深掘りしてみようと思います。

目的は下記の WPT の3 つの周波数帯の違いについて理解を深めることにあります。

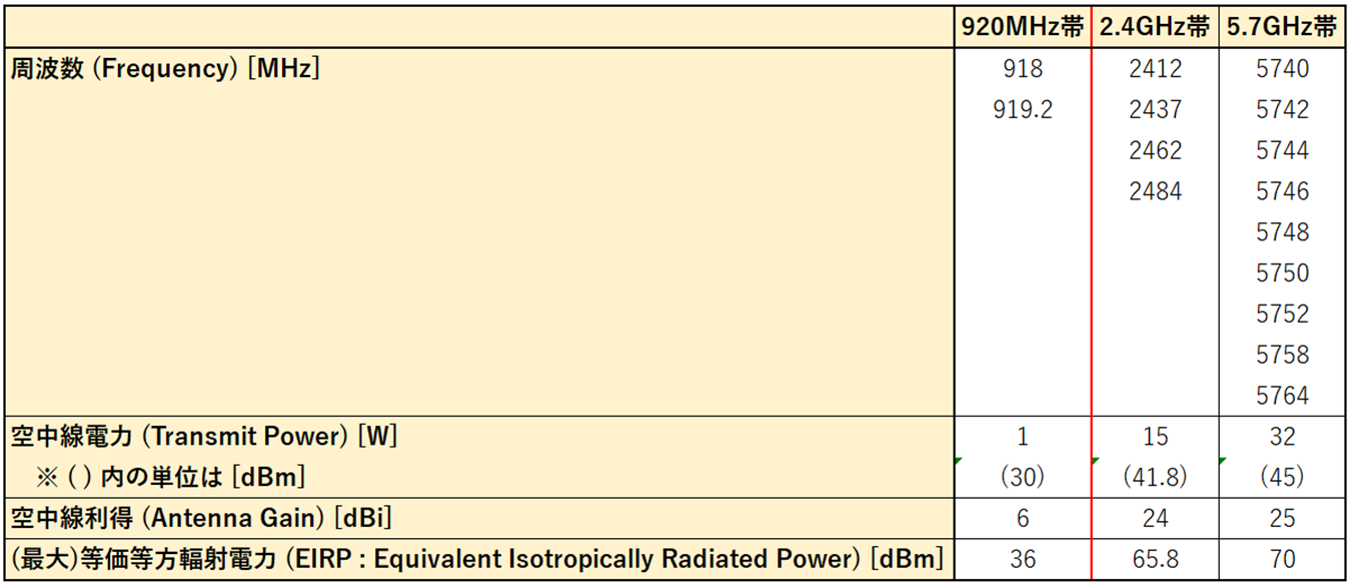
今回は電波伝搬について考えてみたいと思います。

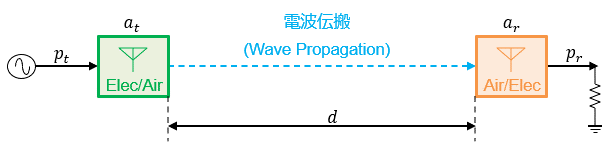
【電波伝搬 (Wave Propagation)】

WPT は電波を用いて電力を伝送します。
電波が空間を伝搬することを電波伝搬 (Wave Propagation) と呼びます。
では、WPT の電波伝搬の考え方は電波を利用する他の無線システム (Wi-Fi や BLE, LTE や 5G のような無線通信システム、レーダーや測距を目的とした無線システム) と異なるのでしょうか？
結論から申し上げると、同じです。電波は物理現象の応用であることから、同じ考え方を適用することができます。

電波の性質は次回以降でまとめてみたいと思いますが、電波伝搬を表現する最も簡単な式をここでご紹介します。フリスの伝達式 (Friis transmission equation) と呼ばれるもので、通信の世界では通信可能距離の概算に用いられます。WPT においても受電電力の概算に使用することができます。
まず、原典とは異なりますが、現在よく用いられている式を下記に示します。

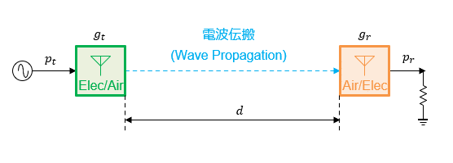
波長 (λ) は前回より λ=c/f だったことから、以下のように変形することができます。

これをdBの単位で表すと

この式は遠方界、かつ自由空間 (誘電体や磁性体が存在しない：真空) における電波伝搬を表す式ですが、経験的に 1m 以上の距離での WPT の能力の概算には有効であると思われます。

d=1m の距離での自由空間伝搬損失は以下の通りです。
920MHz : 31.7dB≒32dB (2.4G帯を基準として －8dB)
2.45GHz : 40.2dB≒40dB
5.75GHz : 47.6dB≒48dB (2.4G帯を基準として +8dB)
この数字を覚えておくと便利ですが、別の機会に暗算する方法も示してみたいと思います。

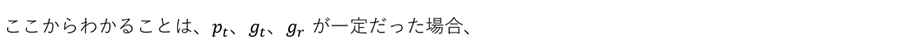
• 受信電力は距離の二乗に反比例する (-6dB/oct, -20dB/dec)
• 受信電力は周波数の二乗に反比例する (-6dB/oct, -20dB/dec) → 周波数が低い方が受信電力は大きい
ということです。

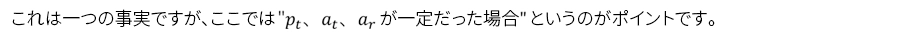
前回アンテナのサイズは一般的に波長に比例する、つまり周波数に反比例すると述べました。
ではアンテナサイズが一定だった場合はどうなるでしょうか？
ここでもう一つのフリスの伝達式 (原典) を示します。

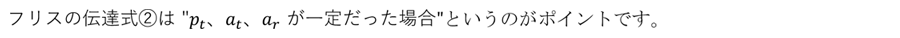
つまり、アンテナの有効開口面積が同じ場合 (同じアンテナサイズの場合)、周波数が高い方が受信電力は大きいということを意味しています。

次回は、電波の性質についてまとめてみようと思います。